Prethodno poglavlje | Pocetna strana | Sledece poglavlje

3. POGONSKI SISTEMI

U ovoj glavi razmotrićemo pogonske sisteme robota. Prvo ćemo dati opšti pregled i karakteristike ranijih i savremenih pogonskih sistema kao i pogled na njihov budući razvoj.

3.1. STANJE I PERSPEKTIVE RAZVOJA

U prethodnim delovima više puta smo spominjali proste industrijske mani-pulatore kao preteću industrijskih robota. Takvi manipulatori koji su opsluživali mašine obično su imali pneumatski pogon. Zglobove manipulatora pokretali su cilindri na bazi komprimovanog vazduha. Takav pogon omogućavao je pouzdan i veoma brz rad uređaja. Bez obzira na te kvalitete pneumatski pogon se vrlo retko sreće kod savremenih robota. Problem je u tome što se takav pogon teško reguliše, odnosno teško je ostvariti kretanje po zadatom zakonu. Ranije smo rekli da manipulatori za opsluživanje mašina nisu ostvarivali neko zadato kretanje već su samo pomerali hvataljku iz jedne tačke u drugu. Za zaustavljanje su korišćeni mehanički graničnici pa se nije postavljao složeniji problem regulacije. Pneumatski pogon pokrene zglob, a zglob se zaustavlja udarom u graničnik. Ovaj vrlo prost način pogona nije mogao zadovoljiti sve veće zahteve, pa se, bez obzira na usavršavanje, pneumatski pogon izbacivao iz upotrebe u robotici. Ipak, treba reći da je u pos-lednje vreme razvijen uspešan pneumatski servo-sistem koji bi mogao zadovoljiti složene zahteve koji se postavljaju pred savremene robote.

Jedan od prvih, a još uvek jednako aktuelnih pogonskih sistema u robotici je hidraulični pogon. U cilindru se nalazi ulje pod pritiskom. Pritisak, posredstvom klipa, pokreće zglob robota. Regulacija kretanja ostvaruje se regulacijom pritiska u cilindru i protoka ulja kroz cilindar. Napajanje cilindra uljem i regulacija protoka vrši se pomoću uređaja koji se naziva servorazvodnik. Kako se u sklopu servorazvodnika nalazi i elektromotor koji pokreće klip razvodnika, to obično govorimo o elektrohidrauličnom pogonu.

Prednosti hidrauličnog pogona su znatne. Pre svega, moguće je ostvariti visoke pritiske u cilindrima, pa time i veoma velike sile u zglobovima robota. Dovoljno je setiti se bagera-kašikara čija "ruka" se pokreće hidrauličnim pogonom. Zahvaljujući toj mogućnosti postizanja velikih sila roboti sa hidrauličnim pogonima nemaju reduktore što znatno pojednostavljuje konstrukciju. Treba još reći da je hidraulični pogon pojednako pogodan i za translatorna i za rotaciona pomeranja.

Najveće prednosti hidraulični pogon iskazuje u primeni kod teških robota. Ovi roboti, namenjeni manipulisanju sa većim teretima (od 100 kg pa i više), moraju ostvariti velike pogonske sile i momente u svojim zglobovima. Hidraulični pogon, za razliku od drugih, vrlo lako ostvaruje takve sile. Pored toga, robot nema reduktor, a nije potrebna ni kompenzacija statičkog opterećenja.

Uz sav opisani značaj koji poseduje hidraulični pogon, u poslednje vreme se uočava tendencija prelaska na električni pogon robota. Ranije je električni pogon korišćen za lake i srednje robote, a danas se i teški roboti sve više projektuju kao električni. Njihova široka upotreba posledica je najpre činjenice da je njihova regulacija relativno jednostavna, a zatim i nekih nedostataka hidrauličnih pogonskih sistema. Hidraulični pogon ima ograničenu maksimalnu brzinu klipa u cilindru, pa je otuda ograničena i brzina robota, a takođe uvek prisutan problem curenja ulja.

Uz konstataciju da se sve više koristi električni pogon robota treba ukazati i na niz problema koje takav pogon donosi. Današnji motori za jednosmernu struju još uvek imaju prilično velike brzine obrtanja (na primer 3000-4000 obrtaja u minuti), a ostvaruju relativno male pogonske momente (na primer do 20 Nm). Zato su neophodni reduktori koji će smanjiti brzinu i povećati momenat. Pre-nosni odnosi reduktora moraju nekada biti prilično veliki (i do 300 puta). Pošto je trenje u reduktoru uvek prisutno, gubi se dobar deo snage (kod dobrih reduktora do 15%), pa je to jedna od nepogodnosti ovakvog pogona. Sledeći problem je mesto postavljanja elektromotora. Da bi se postigla bolja statička uravnoteženost robota motori se Cesto postavljaju tako da su udaljeni od zglobova koje pokreću. Zato je potrebno projektovati mehanizam kojim će se pogon preneti od motora do zgloba. Takav mehanizam ne samo da usložnjava konstrukciju robota već donosi i neke druge probleme kao što je, na primer, problem elastičnih deformacija i oscilacija u prenosnom mehanizmu.

Poseban nedostatak elektromotora jednosmerne struje je postojanje komu-tatora sa četkicama. Kod takve komutacije javlja se varničenje, smanjuje se dozvoljena brzina obrtanja, a dopunska nepogodnost nastaje zbog trošenja četkica. Ovi problemi, međutim, rešavaju se razvojem motora bez četkica (engl. brushless motors) tj. motora sa elektronskom komutacijom.

Kod manjih robota sreću se često i koračni elektro motori (engl. stepping motors), veoma pogodni za povezivanje sa računarom. Međutim, budući da rade u otvorenoj sprezi, još uvek nije razrešeno pitanje njihove potpune pouzdanosti u smislu preciznog pozicioniranja pogotovo u radu sa većim teretima.

Ukažimo sada i na neke nove mogućnosti električnog pogona. Neke su već u potrebi, a neke su stvar blize ili dalje budućnosti. Kako je jedan od glavnih nedostataka elektromotora njihov mali pogonski momenat, a ovaj zavisi od magnetnog polja u motoru, to je usavršavanje usmereno ka razvoju snažnih stalnih magneta čije bi snažno polje omogućilo veći pogonski momenat. Tako se već uveliko proizvode motori sa samarijumom-kobalt magnetima koji su omogućili znatno povećanje pogonskog momenta pri istim dimenzijama motora. To je ipak samo kvantitativni napredak. Nešto kvalitativno novo predstavljaju takozvani motori za direktni pogon. Često se koristi engleski termin direkt drajv (direct drive). Ovi motori, zahvaljujući izuzetno snažnim magnetima i specifičnoj konstrukciji, ostvaruju izuzetno velike pogonske momente, pa više nema potrebe za reduktorom. Takvi motori postavljaju se direktno u zglobove i nema posebnog prenosnog mehanizma. Direkt drajv motori su još u eksperimentalnoj fazi ali se od njih u robotici dosta očekuje.

Još jedna novost u pogonu robota je upotreba motora za naizmeničnu struju. U robotici se pojavljuju tek od skora prvenstveno zbog toga što je regulacija ovih motora, a to znači i upravljanje robotom složenije.

Sada ćemo progovoriti par reči o nekim idejama koje predstavljaju dalju budućnost u oblasti pogona robota. Već smo ranije, govoreći o razvoju robota, uočili da je jedan od osnovnih pravaca njihovog daljeg usavršavanja težnja ka sve većoj univerzalnosti u smislu mogućnosti kretanja. Cilj u dalekoj perspektivi je postizanje pokretljivosti koja bi bila ravna čovekovoj. Otuda sve veća sličnost robota sa čovekom, odnosno sa nekim delovima čovekovog tela (na primer ruka robota) ili pak sličnost sa životinjama (četvoronožne i šestonožne mašine). Zato je prirodna težnja da se dođe do pogonskog sistema koji bi nalikovao mišićima i stoga bio najprikladniji za ovakve konstrukcije.

Mišići čoveka i životinja sastoje se od mišićnih vlakana sposobnih za kontrakciju. Kontrakcijom mišića ostvaruju se sile koje pokreću telo. Ako bismo želeli da ostvarimo veštački pogon sa istim osobinama, odnosno veštački mišić, neophodno je prvo konstruisati jedan tanki izduženi mehanički element sposoban za kontrakciju, dakle veštačko mišićno vlakno. Takvi elementi slagali bi se u snopove i na taj način formirah mišiće.

Ovde možemo povući paralelu između veštačke inteligencije i veštačkog kretanja. Veštačka inteligencija podrazumeva niz metoda kojima se formiraju računarski programi koji su sposobni za određene inteligentne postupke. U pitanju je, na primer, mogućnost učenja, sticanja iskustva i na bazi toga donošenja logičnih i inteligentnih odluka. Zatim, tu su metode prepoznavanja oblika, analize i sinteze govora, itd. Da bi se realizovali svi ovi algoritmi, neophodno je raspolagati digitalnim računarom i on, zajedno sa svim programima, formira elektronski mozak. Osnovni sastavni deo ovakvog mozga je tranzistor, odnosno u novije vreme kompletna složena tranzistorska kola integrisana u minijaturne čipove. Vratimo se sada veštačkom kretanju. Da bi postigli kretanje koje verno odgovara kretanju čoveka ili životinje opet je neophodno raspolagati jednim osnovnim elementom. To bi se moglo nazvati mehaničkim ekvivalentnom tranzistora i u stvari je veštačko mišićno vlakno. Kako smo rekli, to je mehanički element sposoban za kontrakciju. Integri-sanom elektronskom kolu odgovarao bi snop vlakana, dakle mišić. Ova analogija je i strukturna i funkcionalna. Naime, oba ova sklopa sastoje se od osnovnih elemenata koji deluju kao jedna funkcionalna celina.

Danas se na više mesta vrše istraživanja radi razvoja veštačkog mišića. Poznato je, na primer, da je bilo pokušaja da se on realizuje na bazi komprimovanog vazduha. Ipak, možemo reći da do sada nije nađeno pravo rešenje za konstrukciju veštačkog mišića. Tako, ovaj pogon robota ostaje kao ideja koja će se realizovati tek u bližoj ili daljoj

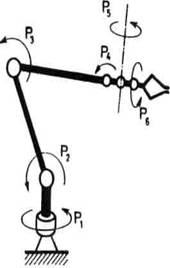
Sl. 3.1. Shema lanaca i shema dejstva  pogona

budućnosti. No, u svakom slučaju, razvoj takvog pogona doprineće daljem povećanju univerzalnosti kretanja robota. U daljem tekstu ove glave razmotrićemo najvažnije tipove pogonskih sistema u robotici. To su: različite vrste elektromotora, hidraulični pogon i pneumatski pogon. Posebnu pažnju obratićemo na mesto postavljanja motora i na način prenosa pogonskog momenta. Konačno, razmotrićemo i mogućnost kompenzacije statičkog opterećenja. Najviše mesta daćemo elektromotorima jednosmerne struje i hidrauličnom pogonu pošto su to danas najčešći pogonski sistemi.

Pogonski motori robota deluju većinom u zglobovima mehanizma izazivajući pome-ranja u zglobovima. Tako, pokrećući zglobove motori pokreću ceo robot.   Na slici 3.1 shematski je prikazan lanac jednog robota i dej-stvo pogonskih momenata označenih sa P_l,P₂, ...,P_n. Kao što se vidi, svaki motor pokreće jedan zglob. Međutim, postoje sheme robota, na primer ASEA-shema, kod   kojih je dejstvo motora znatno složenije (vidi sliku 2.25).

3.2. ELEKTROMOTORI JEDNOSMERNE STRUJE

Kao pogonske elemente u robotici često srećemo elektromotore jednosmerne struje sa stalnim magnetom. Objasnićemo princip rada ovih motora i izvesti matematički model. Ukazaćemo i na različite konstrukcije motora.

Prodiskutovaćemo kasnije način postavljanja motora kod manipulacionih robota i način prenošenja pogonskih momenata od motora od odgovarajućih zglobova.

3.2.1. Princip rada i matematički model

Da bismo objasnili princip rada motora jednosmerne struje sa stalnim magnetom i izveli matematički model poslužićemo se pojednostavljenim modelom prikazanim na sl. 3.2a.

Posmatramo okvir kroz koji protiče struja i, a koji se nalazi u magnetnom polju indukcije B. Na delove okvira AB i CD deluju Lorencove sile

F= i1B                                                      (3.1)

gde je 1 dužina delova AB odnosno BC. Ove dve sile izazivaju spreg sila momenta

    (3.2)

Ovaj momenat izaziva obrtanje okvira oko ose O'O". Vidimo da je proporcionalan struji kroz okvir. Da bi se održao uvek isti smer struje u gornjem i donjem delu okvira, tj. da se ne bi promenio kada deo BC dođe gore, koristi se komutator K. Provodnici C₁ i C₂ koji se naslanjaju na komutator nazivaju se četkice.

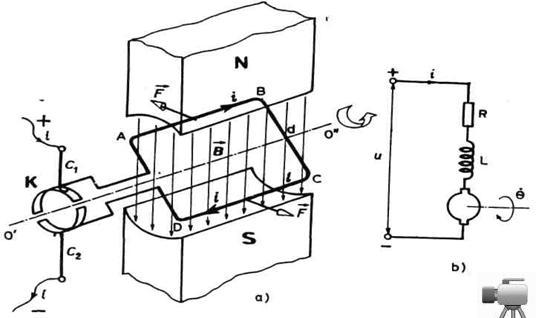
Sl. 3.2. Princip rada motora jednosmerne struje

Opisano obrtanje okvira u magnetnom polju izazvaće indukovanu elektromo-tornu silu u okviru. Intenzitet elektromotorne sile biće:

                            (3.3)

a po smeru je takva da tezi poništavanju struje zbog čega se i naziva kontraelektromotorna sila. Iz izraza (3.3) vidimo da je kontraelektromotorna sila proporcionalna brzini obrtanja . Sada možemo zamisliti više međusobno spojenih okvira koji formiraju rotor motora. Stalni magnet sa postoljem obrazuje stator motora. Ukupni momenat koji će izazvati obrtanje rotora i dalje je proporcionalan struji kroz motor: M = Cmi . Cm je takozvana konstanta momenta čija se vrednost za određeni motor uzima iz kataloga proizvođača.  Kontraelektromotorna sila je i dalje proporcionalna brzini obrtanjatj.. Ce je takozvana konstanta elektromotorne sile.   Može se dokazati da su, u slučaju izražavanja u SI sistemu, ove konstante brojno jednake.Pri tome Cm je izraženo u jedinicama N/A, a Ce u jedinicama V/  .Posmatramo sada dinamičku ravnotežu rotora. Momentu M suprotstavljaju se inercijalne sile rotora momentom gde je I moment inercije rotora, a ugaono ubrzanje. Takođe, suprotstavlja se moment viskoznog trenja M_T = B, gde je B koeficijent, a ugaona brzina rotora i konačno suprotstavlja se momenat P_M spoljašnjeg opterećenja na osovini motora. Momenat P_M nazivamo izlazni momenat motora. Veličine I i B nalaze se u katalozima proizvođača motora. Dinamička ravnoteža sada je data izrazom:

M=M_I+M_T+P_{M k}

odakle sledi

   (3.4)                    

Sada posmatrajmo električnu shemu motora prikazanu na slici 3.2 (b).Priključeni napon u savlađuje kontraelektromotornu silu e, elektrootpornu e_R i kontraelektromotornu silu samoindukcije e_L.

e_R je elektrootporna sila termičke otpornosti namotaja rotora i iznosi e_R = R_i gde je R otpornost, a i struja kroz namotaje. Kontraelektromotorna sila samoindukcije je jednaka e_L = Ldi/dt, gde je L induktivnost. Brojni podaci za veličine R i L uzimaju se iz kataloga. Sada je ravnoteža kola određena izrazom:

u = e + e_L + e_{R k}

tj.

(3.5)

Izrazi (3.4) i (3.5) predstavljaju matematički model motora. Ako je u pitanju motor koji pokreće j-ti zglob robota, tada ovi izrazi dobijaju indeks j:

                                                 (3.6)

    (3.7)

Ove relacije mogu se napisati i u matričnoj kanonskoj formi:

                                               (3.8)

gde je kolona matrica stanja motora dimenzija 3×1:

                                                                    (3.9)

a , i su matrice sistema:

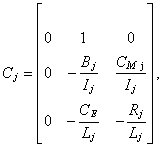
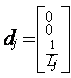                (3.10)

sada možemo reći da relacija (3.8) definiše matematički model motora koji pokreće zglob. Pri korišćenju ovog modela treba voditi računa da je ulazni napon je ograničen po apsolutnoj vrednosti

                                                 (3.11)

Napon  je veličina koju možemo po želji menjati. Tako, napon predstavlja upravljačku promenljivu i menjanjem napona upravljamo kretanjem robota. Ako je induktivnost dovoljno mala () tada je stanje motora određeno vektorom  = i jednačina (3.8) predstavlja matematički model drugog reda u kome su matrice sistema.

Sl. 3.3. Različiti oblici rotora i motora

Sl. 3.4. Motor bez četkicа

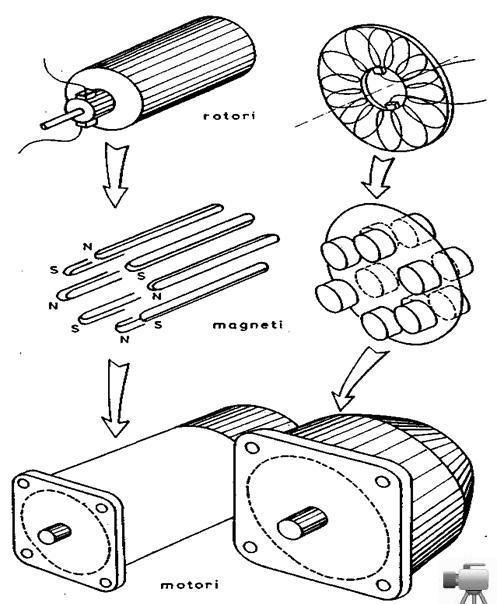
Ukažimo sada na neke različitosti u konstrukcijama postojećih motora. Prvo ćemo reći da se rotori sreću u dva osnovna oblika: cilindričnom i pločastom. Slika 3.3 prikazuje oblik rotora sa metodom komutacije, način postavljanja parova stalnih magneta i spoljašnji izgled motora. Očigledno je da pločasti rotor omogućava kraću ali širu formu motora.

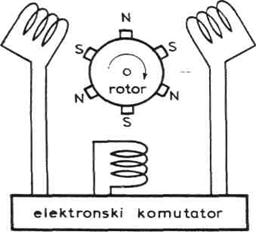
Moguće je i zameniti uloge rotora    i statora. Tada se na rotoru nalaze parovi stalnih magneta, a na statoru namotaji kroz koje protiće struja. Shema je prikazana na slici 3.4. Očigledno, tada ne postoji komutator sa četkicama pa se izmena smera struje u namotajima obezbeđuje posebnim elektronskim sistemom. Zato govorimo o elektronskoj komutaciji i elektronskom komutatoru. Ovakve motore bez četkica nazivamo često i engleskim terminom brašles (brushless) motori. Elektronska komutacija omogućava motorima znatno veće radne brzine, izbegnut je problem trošenja četkica, kao i varničenja. Treba reći da ovakva komutacija nije jednostavna. Učestanost promene smera struje mora biti usklađena sa brzinom obrtanja motora.

3.2.2. Načini postavljanja motora

U ovom delu razmotrićemo način i mesto postavljanja motora koji pokreću zglobove robota.

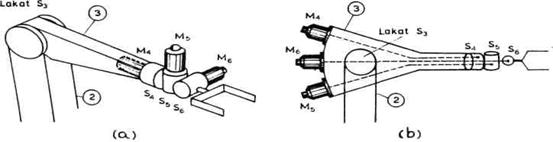
Analizu ćemo početi od zglobova šake. Na slici 3.5 a prikazan je treći segment minimalne konfiguracije i segmenti šake i jedan mogući način postavljanja motora. Motori su postavljeni direktno u zglobovima koje pokreću. Na slici, motori koji pokreću zglobove S₄,S₅,S₆ označeni su M₄,M₅,M₆. Ovaj način omogućava jednostavnu konstrukciju, međutim, ima dosta nedostataka. Šaka postaje glomazna i to sa jedne strane povećava opterećenje robota, a sa druge strane smanjuje mogućnosti kretanja zglobova šake.

Sl. 3.5. Načini postavljanja motora za pogon šake

Drugi način, koji je češći, polazi od ideje da motore treba postavljati što bliže osnovi robota jer se tako smanjuje statičko opterećenje. Kada su u pitanju zglobovi šake i motori koji ih pokreću, jedan raspored motora koji sledi ovu ideju prikazan je na slici 3.5(b). Motori su postavljeni iza lakta i predstavljaju kontratežinu. Pogonski momenti se od motora prenose osovinama do odgovarajućih zglobova.

Sl. 3.6. Načini postavljanja motora za pokretanje minimalne konfiguracije

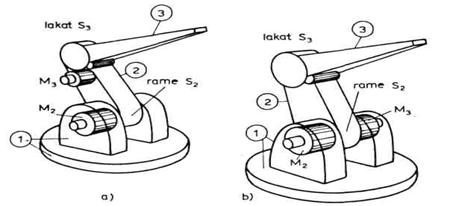
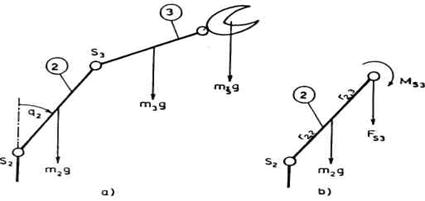
Analiziraćemo pogon zglobova minimalne konfiguracije. Razmotrimo prvo zglobove S₃ i S₂ tj. lakat i rame robota (sl. 3.6.). Jedna od mogućnosti je smeštanje motora uz same zglobove kao što je prikazano na slici 3.6(a). Ovakav pristup pojednostavljuje konstrukciju prenosa pogonskog momenta od motora na zglob. Primetimo da ovde svaki motor deluje između dva susedna segmenta. M₃ pokreće zglob S₃, i deluje između segmenata 2 i 3 tako što stator vezujemo za segment 2, a rotor preko određenog prenosnog mehanizma za segment 3. Slično važi za motor M₂ koji deluje između segmenta 1 i 2. Ovo je shematski prikazano na slici 3.7(a). Razmotrićemo još jednu mogućnost. Motori M₂ i M₃ mogu se postaviti na mesta prikazana na slici 3.6(b). Za motor M₂ koji pokreće rame S₂ važi sve što je malopre rečeno, ali pitanje motora M₃ je složenije. Ovaj motor pokreće lakat S₃. Svojom osovinom rotora, preko prenosnog mehanizma, motor je vezan za segment 3. Stator motora može se vezati na dva različita načina. U prvom slučaju stator vezujemo za segment 2 i time dobijamo da motor M₃ deluje između segmenata 2 i 3. Ovaj slučaj je, dakle, po dejstvu motora ekvivalentan načinu prikazanom i opisanom pod (a). Ovo je shematski prikazano na slici 3.7(b).

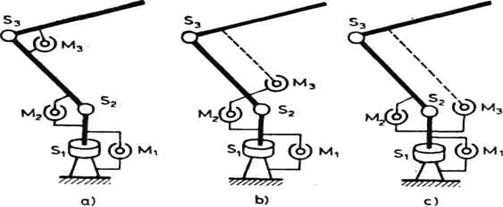
Sl. 3.7. Otvoreni i zatvoreni lanci

U drugom slučaju stator motora M₃ vezujemo za segment 1. Tada motor deluje između segmenata 1 i 3. Na ovaj način dobijamo vezu između segmenata koji nisu susedni (sl. 3.7c).

Ostalo je i da razmotrimo zglob S₁ tj. obrtanje robota oko vertikalne ose. Taj zglob vezuje segment 1 sa podlogom i motor M₁ se uvek vezuje između tih segmenata. Pri tome stator može biti učvršćen na segmentu 1 ili na podlozi.

Trebalo bi spomenuti i poseban način pogona minimalne konfiguracije koji se javlja kod ASEA-sheme (vidi sliku 2.25).

3.2.3. Prenos pogonskog momenta

Problem prenosa pogonskog momenta od motora do zgloba je važno i dosta opširno pitanje. Naime, postoji veliki broj različitih rešenja prenosnog mehanizma i nemoguće ih je sve predstaviti. Zato ćemo se ovde zadržati na nekoliko primera koji su relativno često korišćeni. Tako čitalac dobija određenu predstavu o ovom problemu. Kao prvo uočavamo sledeće: motori jednosmerne struje daju male momente i velike brzine obrtanja. Ove pojmove malo i veliko treba shvatiti uslovno. Mislimo da su momenti mali u odnosu na momente koji su potrebni za pokretanje robota, a brzine su velike u odnosu na brzine kojima se obrću zglobovi robota pri nekom uobičajenom kretanju. Zbog ovoga prenosni mehanizam uvek sadrži reduktor koji u određenom odnosu povećava pogonski momenat (na primer N puta) i u istom odnosu smenjuje brzinu obrtanja (takođe N puta). Ovaj odnos naziva se prenosni odnos reduktora, ili stepen redukcije. Najjednostavnija realizacija reduktora je u obliku para zupčanika (sl. 3.8) čiji su poluprečnici u odnosu 1:N.

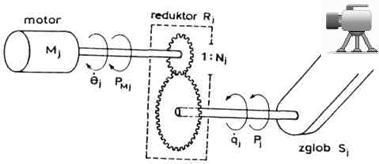
Sl. 3.8. Prenos  pogonu preko reduktora

Posmatrajmo zglob. Ako je na izlazu motora momenat, ugao obrtanjai brzina obrtanja , tada će moment u zglobu P_j, ugao u zglobu , i brzina biti:

       (3.13)

    (3.14)

    (3.15)

gde je  prenosni odnos reduktora.

U praksi, da bi se ostvario željeni prenosni odnos reduktora neophodno je redovno vezati nekoliko parova zupčanika i tako u nekoliko koraka ostvariti željenu redukciju. Naime, jasno je da se ne može praviti par zupčanika čiji bi poluprečnici bili u odnosu, na primer, 1:300. U slučaju više parova javlja se problem zazora. U svakom kontaktu dva tela, pa tako i zupčanika, javlja se prazan hod ili zazor, dakle malo pomeranje koje ne možemo kontrolisati. Otuda je poželjno izbegavati veći broj parova zupčanika da se zazor ne bi umnožavao. Jedan način da se ovaj problem reši je konstrukcija specijalnih vrsta reduktora koji uspevaju da ostvare velike prenosne odnose sa jednim ili bar sa malim brojem zupčastih parova. Od takvih konstrukcija u robotici se najčešće koriste tzv. harmonik drajv (harmonic drive) reduktori. Princip rada ovih reduktora objasnićemo koristeći sliku 3.9.

Osnovni funkcionalni delovi su ulazna elipsa označena na slici sa (e), takozvani generator talasa (engleski: wave generator) označen sa (g) i kućište (k). Između elipse i generatora talasa nalazi se eliptični kuglični ležaj, pa je tako omogućeno međusobno obrtanje ova dva elementa, a generator i kućište su u zupčastoj vezi. Osovina motora učvršćuje se za elipsu koja se onda obrće brzinom motora . Tako  predstavlja ulaznu brzinu reduktora. Kućište ćemo smatrati nepokretnim i tada će zupci kućišta određivati obrtanje generatora. Generator je od elastičnog materijala i obrće se stalno menjajući pravac deformacije. Generator se vezuje za izlaznu osovinu reduktora. Ova osovina pokreće zglob robota, pa njenu brzinu označavamo sa . Da bismo jasno prikazali odnos ulazne brzine  i izlaza poslužićemo se prvo jednim pojednostavljenjem. Pretpostavićemo da je broj zuba generatora za jedan manji od broja zuba kućišta. To znači da, ako se ulazna elipsa obrne za pun krug, utiskujući pri tom zube generatora u zube kućišta, generator će se pomeriti za jedan zub unazad. Proizlazi da je obrtanje generatora znatno sporije. Ako se posmatra uopšteno, generator će se obrnuti unazad za onoliko zuba koliko ih ima manje nego na kućištu. Neka je to . Ugao obrtanja je taka , gde je  ugao koji odgovara jednom zubu. Dakle, ako se ulazna osovina obrne za pun krug tj.  onda će se izlazna osovina obrnuti unatrag za q =. Prenosni odnos reduktora N =/q sada postoje:

     (3.16)

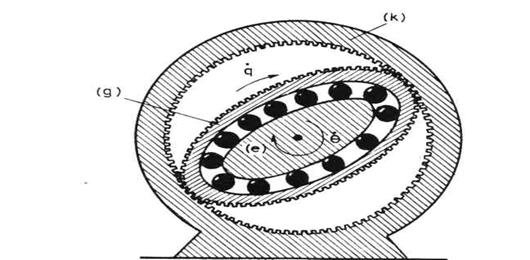
Sl. 3.9. Harmonik drajv reduktor

U ovom odnosu smanjuje se izlazna brzina i povećava izlazni moment.

Treba još reći da se harmonik drajv reduktori odlikuju jako malim zazorom ali se s druge strane mora voditi računa o uvijanju reduktora pri prenosu većih opterećenja.

Do sada smo smatrali da se pogonski momenat povećava u istom odnosu u kome se smanjuje brzina. Međutim, zbog unutrašnjih trenja u reduktoru gubi se deo snage. To se uzima u obzir tako što prenosni odnos brzine ostaje N, a prenosni odnos momenta postaje , gde je  takozvani koeficijent korisnog dejstva reduktora, tj. odnos izlazne i ulazne snage. Sada relacija (3.13) postaje:

 (3.17)

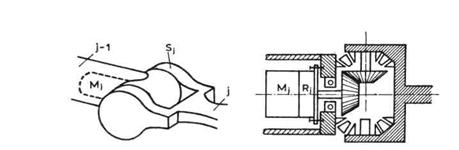
Sl. 3.10. Jedan zglob robota

Sl. 3.11.    Laktasta shema manipulacionog robota

Koeficijent  je uvek manji od jedinice jer je izlazna snaga manja od ulazne. Kod harmonik drajv reduktora koji se odlikuju visokim koeficijentom korisnog dejstva on može iznositi okvirno od 0,6 do 0,9.

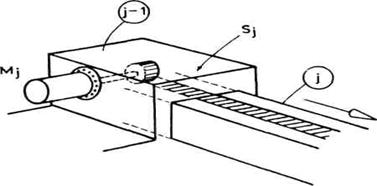
Sada ćemo prikazati nekoliko primera prenosnih mehanizama za pogon manipulacionih robota. Slika 3.10 prikazuje spoljni izgled jednog zgloba i moguću shemu pogona toga zgloba. Reduktor  direktno se nastavlja na motor tako da možemo govoriti o sklopu motor-reduktor. Stator ovog sklopa učvršćen je za segment "j-1", a rotor, preko izlazne osovine i para zupčanika, za segment "j". Ovde očigledno ne postoji neki složen prenosni mehanizam.

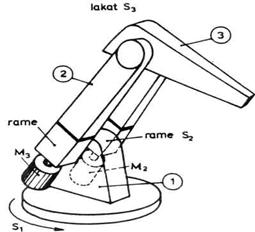
Na slici 3.11 prikazan je spo-ljašnji izgled jedne minimalne konfiguracije robota laktaste sheme.

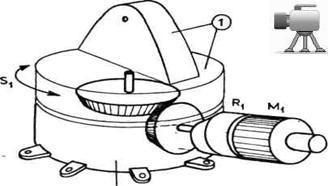
Na slici 3.12 prikazana je shema pogona zgloba S₁ koji predstavlja obrtanje celog robota oko vertikalne ose. Stator je učvršćen za postolje, a rotor, preko osovine i para zupčanika, obrće segment 1, a time i ceo robot.

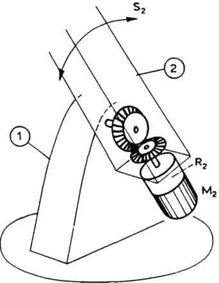
Na slici 3.13 prikazana je shema pogona ramena S₂. Sklop motor- reduktor (M₂ — R₂) preko zupčastog para pokreće zglob. Stator je vezan za segment 2, a rotor preko zupčanika za segment 1.

Sl. 3.12. Shema pogona zgloba S₁

Sl. 3.13. Shema  pogona ramenog zgloba

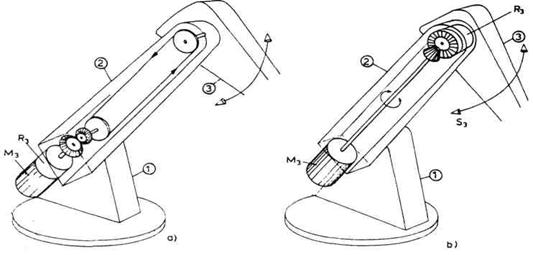
Na slici 3.14 prikazane su dve moguće realizacije prenosa pogona na zglob lakta S₃. U slučaju (a) motor M₃ i reduktor R₃ vezani su u jedinstven sklop. Stator je učvršćen za segment 2. Rotor pokreće par zupčanika, a zatim se pogon prenosi preko prenosnog lanca do segmenta 3. U ovoj varijanti i motor i reduktor smešteni su blizu osnove robota čime je smanjeno opterećenje. Mana ovog prenosa je što se svaki zazor lanca ili njegovo elastično istezanje pokazuje direktno kao greška u pomeranju segmenta 3. Ovo posebno treba imati u vidu ako se zna da u ovom slučaju lanac prenosi veliku silu jer se radi o pogonu iza reduktora. Slučaj (b) ispravlja ovu manu. Prvo uočavamo da su motor i reduktor sada razdvojeni. Pogonski momenat motora M₃ prenosi se osovinom do zgloba lakta, gde preko para zupčanika ulazi u reduktor R₃. Izlazna osovina reduktora vezuje se i pokreće segment 3. Ovde primećujemo da prikazana dugačka osovina prenosi mali momenat jer se radi o momentu motora pre reduktora. Eventualna greška usled zazora i elastičnog uvijanja osovine posredstvom reduktora smanjuje se N puta. Tako, ovakav prenos omogućava manje greške koje bi bile posledica zazora ili elastičnih deformacija. S druge strane, u ovom slučaju smo reduktor udaljili od osnove robota i time povećali opterećenje.   Ovde nismo imali kao cilj diskusiju o prednosti jedne ili druge varijante prenosa već su nam obe varijante služile samo kao ilustracija različitih mogućnosti.

Sl. 3.14. Dve mogućnosti za prenos pogona  zgloba lakta

Sl. 3.15. Pogon translatornog zgloba

Sledeći primer odnosi se na pogon translatornog zgloba. Slika 3.15 predstavlja jednu mogućnost za pokretanje translatornog zgloba. Stator motora ućvršćen je za segment "j-1", a rotor preko osovine, jednog zupčanika i zubaca na segmentu "j", pokreće segment "j". Drugi čest način pokretanja translatornih zglobova je pomoću zavojnih vretena.

3.3. MOTORI NAIZMENIČNE STRUJE

Motori za naizmeničnu struju u robotici se još uvek sreću rede nego motori za jednosmernu struju, bez obzira na njihove veoma dobre pogonske karakteristike i jednostavnu konstrukciju. Glavni problem leži u složenosti regulacije ovih motora. Međutim, razvojem elektronike i postupaka regulacije servo-motori za naizmeničnu struju koriste se sve više. Objasnimo princip rada asinhronog (indukcionog) i sinhronog motora.

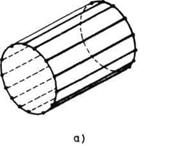
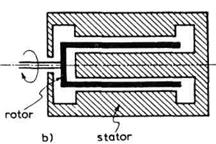
Sl. 3.16. Kavezni rotor (a) i motor sa rotorom oblika šolje (b)

Asinhroni motor za naizmeničnu struju sastoji se od rotora i statora. Na statoru se nalaze namotaji koji se priključuju na izvor naizmenične struje. Rotor motora je kratko spojen, dakle, nema komutatora i četkica. Rotor motora može biti motan (sa željenim brojem faza) ili, što je češće, može biti kaveznog tipa. Kavezni rotor (sl. 3.16a) sastoji se od šipki koje su na krajevima povezane provodnim prstenovima. Konačno, rotor može biti oblika šolje (sl. 3.16b) što omogućava smanjenu masu i inerciju zato što gvozdeno jezgro više nije u sastavu rotora.

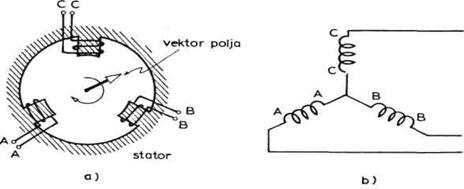
Sl. 3.17. Obrtno magnetno polje - shema trofaznog statora (a) vezanog u zvezdu (b)

Objasnimo prvo takozvano obrtno magnetno polje koje je ključni efekat za rad indukcionog motora. Ako stator sa trofaznim namotajima (sl. 3.17) priključimo na izvor trofazne naizmenične struje (fazna razlika 2/3), u unutrašnjoj će se obrazovati tzv. obrtno magnetno polje. Možemo ga predstaviti vektorom konstantnog intenziteta koji se obrće ugaonom brzinom = 2, gde je  frekvenca struje. Ovu brzinu zovemo sinhrona brzina. Obrtno polje možemo postići i dvofaznim sistemom (fazna razlika /2) ako se polovi postave kao što je prikazano na slici 3.18.

Sl. 3.18. Obrtno magnetno polje - shema dvofaznog statora

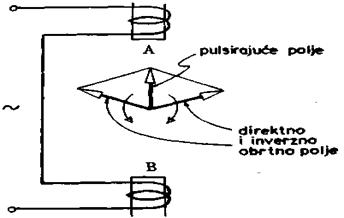
Sl. 3.19. Monofazni stator i magnetno polje

U slučaju monofaznog napajanja statora (sl. 3.19) dobija se pulsirajuće magnetno polje stalnog pravca (AB na slici). Ovakvo polje, koje nije obrtno, može se posmat-rati kao superpozicija dva obrtna polja koja se obrću u različitim smerovima, a intenziteti su im jednaki polovini amplitude pulsirajućeg polja. Ova obrtna magnetna polja nazivaju se direktno i inverzno polje. Stvar je slobodnog izbora koje će se polje smatrati direktnim.

Zamislimo sada kratkospojeni rotor na koji deluje obrtno magnetno polje. Polje će tada presecati kolo rotora i u provodnicima rotora indukovaće se struja, a za tim Lorencova sila koja će pokrenuti rotor u smeru obrtanja polja. Pri obrtanju rotora njegova brzinabiće manja od brzine obrtanja magnetnog polja(tj. od sinhrone brzine). Ova razlika naziva se brzina klizanja, a često se izražava  relativnoi naziva klizanje.

Struja u rotoru izazvaće svoje magnetno polje. Može se pokazati da će se polje rotora, bez obzira na klizanje rotora, obrtati sinhronom brzinom. Tako, sabiranjem polja statora i rotora formira se rezultujuće polje koje se obrće sinhronom brzinom. Kako ovo polje seče kolo rotora (zbog klizanja) održava se indukcija u rotoru. Dejstvom rezultantnog polja na rotor sa strujom (Lorencove sile) pojavljuje se obrtni moment na osovini rotora. Očigledno, moment postoji sve dok postoji klizanje. Ako bi se rotor obrtao sinhronom brzinom, prestala bi indukcija i rotoru, a time nestao i momenat. Ukupno, možemo reći da obrtno magnetno polje "vuče" rotor i on se obrće u smeru obrtanja polja. U slučaju monofaznog motora kod koga postoji direktno i inverzno obrtno polje, rotor može pratiti bilo koje od njih. Zato se koristi posebno pokretačko kolo tj. dopunski namotaji koji povuku rotor u željenom smeru. Nakon postizanja određene brzine centrifugalni prekidač isključuje pokretačko kolo. Karakteristika svih indukcionih motora je njihova težnja da se obrću konstantnom brzinom. Ukoliko se želi ostvariti promenljiva brzina, kao što je slučaj kod primene u robotici, to se postiže menjanjem napona i frekvence napajanja motora. Sinhroni motor za naizmeničnu struju ima trofazne namotaje na statoru dok je rotor ili u obliku stalnog magneta ili u obliku namotaja napajanih jednosmernom strujom. U savremenim servosistemima se, po pravilu, sreću motori sa stalnim magnetima. Shema motora prikazana je na slici 3.4. Dakle, konstrukcija je shematski slična konstrukciji motora jednosmerne struje sa elektronskom komutacijom. Suštinska razlika je u tome što se statorski namotaji ne napajaju elektronski komutiranom jednosmernom strujom, već trofaznom naizmeničnom strujom. Stator sa trofaznom strujom stvara u motoru obrtno magnetno polje sinhrone brzine . Ovo polje deluje na polove stalnog magneta stvarajući momenat oko osovine motora. Rotor će se obrtati istom brzinom kao i polje ali će zaostajati za određeni ugao  koji je utoliko veći ukoliko je veće opterećenje na osovini motora.

Regulacija brzine ovih motora ostvaruje se promenom frekvence napajanja statora čime se menja sinhrona brzina. Ovi motori su relativno skoro ušli u širu primenu kod robotskih sistema. Razlog leži u složenosti regulacije ovog pogona. Međutim, savremena elektronika omogućava uspešnu regulaciju ovih motora i to u veoma širokom opsegu (od brzine O do nekoliko hiljada obrtaja u minuti). Budući da sinhroni motori imaju veoma dobre pogonske karakteristike (stalan momenat u širokom opsegu brzina) njihova primena u robotici doživljava nagli rast.

3.4. KORAČNI MOTORI

Jedna veoma specifična vrsta elektromotora su takozvani koračni motori (engleski stepper motors, stepping motors). Naziv dolazi otuda što se oni kreću u vidu niza diskretnih uglova pomeraja-koraka. Kako se brojem ovih koraka može upravljati, to na taj način ostvarujemo i upravljanje položajem i nije potrebna povratna sprega. Zato kažemo da se ovi motori koriste u otvorenoj sprezi. S obzirom na to da se upravlja diskretnim pomeranjima, ovi motori su veoma pogodni za sprezanje sa upravljačkim računarom. Obično se koriste kod robota manjih nosivosti.

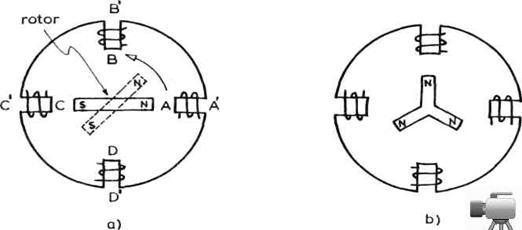
Sl. 3.20 Dve vrste koračnih motora

Objasnimo princip rada ovih motora na primeru prikazanom na slici 3.20a. Kada se kroz namotaje AA' propusti struja, tada kraj A postane južni pol elektromagneta. Rotor sa stalnim magnetom će se tada postaviti tako da mu severni pol (N) bude naspram tačke A. Ako se sada struja propusti kroz namotaje BB', a ostavi se da teče kroz AA', tada će A i B biti južni polovi. Rotor će se sada obrnuti za 45° i postaviti tako da severni pol bude između A i B. Sada se isključuje struja u namotajima AA', pa će se rotor obrnuti još za 45° da bi severni pol bio naspram tačke B. Ovakav postupak se nastavlja dok rotor ne obrne pun krug. Tako dobi-jamo obrtanje rotora sa konačnim korakom koji iznosi 45°. Korak se može smanjiti povećavanjem broja polova na statoru. Jedan drugačiji tip koračnog motora prikazan je na slici 3.20b. Prikazani motor ima korak od 30°, a korak se može smanjiti povećanjem broja polova. Kod koračnih motora digitalni izlaz iz upravljačke jedinice (signali napona ±5V) treba dovesti na prekidačku shemu koja će obezbediti proticanje struje iz izvora napajanja kroz određenje namotaje.

3.5. ELEKTROHIDRAULIČNI POGON

U prethodnim odeljcima videli smo da se kod robota pokretanih elektromotorima, a namenjenih za rad sa većim teretima javljaju određeni problemi. Potrebni su reduktori sa velikim prenosnim odnosima i mora se voditi računa o uvijanju reduktora kao i o elastičnoj deformaciji prenosnog mehanizma. Hidraulični pogoni prikladni su za ovakve namene jer se opisani problemi u njihovom slučaju ne javljaju. To je otuda Sto hidraulični pogoni mogu ostvariti veoma velike sile i momente, pa reduktori nisu potrebni ni za najveća opterećenja. Pogoni se tako i postavljaju da nije potreban složen prenosni mehanizam. U ovom odeljku opisaćemo princip rada i matematički model hidrauličnih motora i način njihovog postavljanja kod robotskih sistema.

3.5.1. Komponente i princip rada

Elektrohidraulički pogonski sistem sastoji se, u principu, od hidrauličkog cilindra sa klipom i servorazvodnika sa magnetnim motorom.

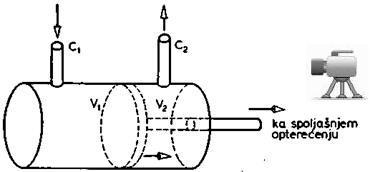
Sl. 3.21. Hidraulički cilindar

prikladni su za ovakve namene jer se opisani problemi u njihovom slučaju ne javljaju. To je otuda Sto hidraulični pogoni mogu ostvariti veoma velike sile i momente, pa reduktori nisu potrebni ni za najveća opterećenja. Pogoni se tako i postavljaju da nije potreban složen prenosni mehanizam. U ovom odeljku opisaćemo princip rada i matematički model hidrauličnih motora i način njihovog postavljanja kod robotskih sistema.

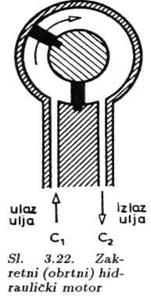
Cilindar sa klipom prikazan je na slici 3.21. Napajanje se vrši hidrauličkim uljem veoma male stišljivosti. Ako se ulje pod pritiskom dovodi na ulaz C₁ tada će se klip pome-rati udesno. Zapremina V₁ će se povećavati, a V₂ smanjivati. Kroz izlaz C₂ oticaće ulje iz cilindra. Ukoliko želimo da ostvarimo kretanje ulevo, promenićemo smer protoka ulja. C₂ postaje ulaz, a C₁ izlaz. Protok i razlika pritisaka određuju ne samo smer već i brzinu kretanja klipa. Klip dalje vezujemo za određene spoljašnje mehanizme koje želimo pokrenuti i koje nazivamo spoljašnjim opterećenjem (na primer zglob robota).

Na istom principu moguće je ostvariti i obrtno kretanje (sl. 3.22). Umesto klipa postoji rotor sa krilima. Tako, ostvarujući pritisak na krilo rotora, dobijamo obrtno kretanje. Shema na slici 3.22 omogućava obrtanje za ugao od približno 360°. Drugačije konstrukcije, međutim, omogućavaju konti-nualno obrtanje bez ograničenja.

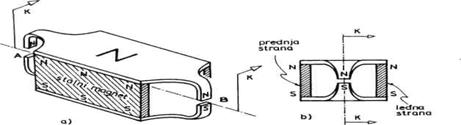
Servorazvodnik se sastoji od razvodnika i magnetnog motora sa opružnom povratnom spregom. Objasnimo prvo konstrukciju i način rada motora. Na prednjoj i leđnoj strani (sl. 3.23.) postavljena su uspravno dva pločasta stalna magneta.

Ovim se postiže da cela gornja ploča bude severni pol (N), a donja južni pol (S). U prorezima A i B javiće se sada jako magnetno polje. U unutrašnjost konstrukcije smešta se kotva sa namotajima. Presek K- K označen na slici 3.23. prikazan je na slici 3.24.

Sl. 3.23. Konstrukcija  magnetnog motora

Sl. 3.24. Princip rada  magnetnog motora

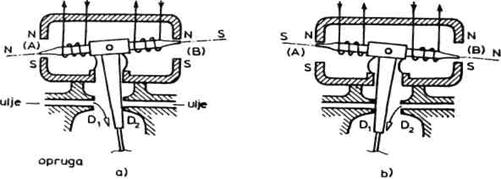
Ako se kroz namotaje pusti struja smera prikazanog na sl. 3.24a, na kraju A će se indukovati severni, a na kraju B južni pol. Usled toga kotva će se obrnuti ulevo. Ako se smerovi struja promene (sl. 3.24b), kotva će se obrnuti udesno. Zajedno sa kotvom pomera se i leptir koji zatvara desni ili levi dovod ulja (D₁,D₂) kao što je prikazano na slici 3.24. Pretpostavimo da je kroz namotaje puštena struja i i da se kotva obrnula ulevo pomerajući leptir udesno i time zatvarajući otvor D₂ za protok ulja (sl. 3.25a). Sada ulje kroz desnu liniju ostvaruje pritisak na desnu stranu klipa razvodnika i on se pomera ulevo (pomeranje z). Desni glavni dovod ulja P_n2 je sad zatvoren. Iz levog glavnog dovoda P_nl i kroz vod C₁ ulje protiče u cilindar. Klip cilindra pomera se udesno (pomeranje s), a ulje otiče kroz cev C₂ i povratni vod R. Pomeranjem klipa pomeraju se i spoljašnji mehanizmi vezani za klip.

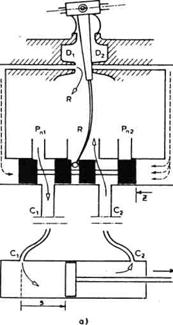
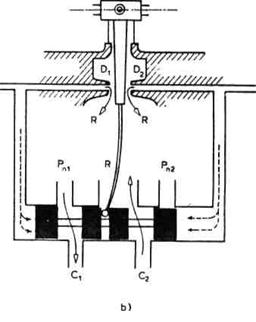
Sl. 3.25. Cilindar sa servorazvodnikom

Pomeranjem razvodnika ulevo dolazi do elastične deformacije opruge povratne sprege. Pri određenoj veličini deformacije elastični momenat počeće da po-mera leptir ulevo čime se delimično otvara dovod D₂ . Proticanje ulja kroz D₂ smanjiće pritisak sa desne strane klipa razvodnika no, on je još uvek veći od pritiska sa leve strane, pa klip nastavlja kretanje ulevo. Pritisci se izjednačuju kada se izjednače protoci kroz D₁ i D₂ tj. kad leptir bude vertikalan a kotva motora horizontalna (sl. 3.25b). Klip razvodnika se zaustavlja i u tom položaju (z) uspostavljena je ravnoteža momenta motora i elastičnog momenta opruge. Tom položaju razvodnika odgovara određeni protok iz glavnog dovoda P_nl kroz cilindar, a time i određena brzina pomeranja klipa u cilindru. Kako moment motora zavisi od struje i, to možemo reći da protok kroz cilindar (i kretanje klipa z) zavisi od struje motora. Promenom struje promenićemo moment motora, pomeriti razvodnik (tj. promeniti z) i tako promeniti protok kroz cilindar.

3.5.2. Matematički model

Pri izvođenju matematičkog modela hidrauličnog pogonskog sistema uvešćemo određena uprošćenja. Simetričan cilindar (sl. 3.26) obezbeđuje da površine klipa sa obe strane budu jednake i pojednostavljuje račun. Takođe, zanemariće se dinamika servorazvodnika.

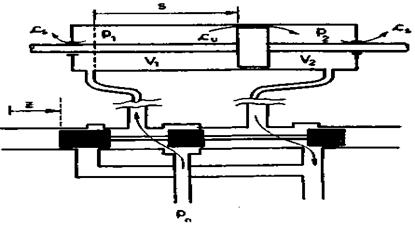
Sl. 3.26. Simetrični cilindar

Posmatrajmo dinamičku ravnotežu klipa u cilindru. Neka su p₁ i p₂ pritisci ulja sa jedne i druge strane klipa, a A slobodna površina klipa (jednaka sa obe strane). Tada na klip deluje sila pritiska

        (3.18)

gde je p_d=p₁-p₂ razlika pritisaka (diferencijalni pritiska). Ovoj sili suprotstavlja se inercijalna sila klipa , gde je m masa, w ubrzanje, a s  koordinata pomeranja klipa (sl. 3.26). Zatim se suprotstavlja sila viskoznog trenja F_T = B, gde je B koeficijent, a brzina. Konačno, sili F se suprotstavlja sila F_M spoljašnjeg opterećenja. F_M predstavlja izlaznu silu hidrauličnog pogona. Dinamička ravnoteža data je izrazom

    (3.19)

tj.

          (3.20)

Sada ćemo posmatrati protok ulja kroz cilindar i označićemo ga sa Q. Zapreminski protok definišemo kao količnik protekle zapremine ulja i vremena. Za cilindrične zapremine, ovaj količnik će postati proizvod površine poprečnog preseka i brzine: A. Međutim, zbog curenja i zbog sabijanja (kompresije) ulja, ovom protoku će se dodati dopunski sabirci: cpd zbog curenja i  zbog kompresije.Objasnićemo ove izraze. Curenje ulja je posledica pritiska i zato uvodimo koeficijent curenja (c) kao protok curenja za jedinični pritisak. Curenje delimo na unutrašnje i spoljašnje. Unutrašnje predstavlja prolaz ulja pored klipa, sa jedne strane na drugu, i dešava se unutar cilindra. Spoljašnje curenje predstavlja prolaz ulja pored vodica u spoljašnju sredinu (sl. 3.26). Tako je koeficijent , gde je cu koeficijent unutrašnjeg, a  cs spoljašnjeg curenja. Za kompresiju ulja treba reći da je mala i da koeficijent stišljivosti β zavisi od procenta vazduha u ulju. Sada za protok možemo napisati

      (3.21)

V predstavlja ukupnu zapreminu tj. V =  V₁  + V₂ (što uključuje cilindar, cevi, servorazvodnik).

Protok se, kako je već rečeno, reguliše servorazvodnikom. Nelinearna statička karakteristika servorazvodnika (protok u funkciji pritiska) ima oblik

    (3.22)

gde z predstavlja pomeranje klipa servorazvodnika, sgn (z) njegov znak (+ ili -), pn pritisak napajanja, w gradijent povećanja površine sa pomeranjem klipa, ρ gustinu ulja i D bezdimenzioni koeficijent. Ako je masa klipa razvodnika mala (dakle veliki propusni opseg) tada možemo zanemariti njegovu dinamiku i pomeranje z smatrati proporcionalnim struji magnetnogmotora tj:

   (3.23)

gde je C_M konstanta momenta magnetnog motora, a γ elastični koeficijent momenta opruge. Ovo se dobija na osnovu ravnoteže momenta motora i opruge: C_Mi = γ z.

Tako smo došli do matematičkog modela elektrohidrauličnog pogona koji je definisan relacijom (3.20) - (3.23). Dobijeni model je nelinearan.

Linearizacija karakteristike servorazvodnika (3.22) u okolini radne tačke T daje

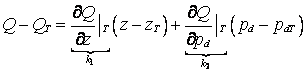             (3.24)

a uz uslov simetrije dobija se dalje

                                                                  (3.25)

Sada relacija (3.20), (3.21), (3.23), (3.25) određuju linearni oblik matematičkog modela. Model je trećeg reda, a koordinate stanja su

                                                                      (3.26)

Dobijeni linearni model može se napisati i u kanonskom obliku

                                          (3.27)

gde je dodat indeks "j" da bi odredio zglob robota koji se posmatranim cilindrom pokreće. Matrice sistema su:

k

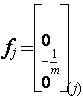;  (3.28)

3.5.3. Način postavljanja motora

U ovom odeljku razmotrićemo, pomoću nekoliko primera, način postavljanja hidrauličnih pogona za robot. Videli smo već da hidraulični motori mogu biti kon-struisani tako da kao izlaz daju ili translatorno ili obrtno kretanje. Kako zglobovi robota mogu biti translatorni ili obrtni, to izgleda logično da se translatorni motori, dakle cilindri, koriste za pogon translatornih zglobova, a rotacioni motori za pogon rotacionih zglobova. Međutim, hidraulični cilindri se često koriste za pogon i translatornih i rotacionih zglobova.

Razmotrimo prvo slučaj rotacionih hidrauličnih motora. Oni se uglavnom postavljaju u zglobove robota gde bez reduktora ostvaruju traženi pogonski mo-menat. To je moguće zahvaljujući velikom izlaznom momentu i maloj brzini ovih motora. Može se još reći da postoje i takozvani brzohodni hidraulični motori koji se odlikuju velikom brzinom i manjim izlaznim momentom. Kod takvih motora reduktor je neophodan, pa je njihova primena unekoliko slična primeni elektromotora.Posmatrajmo zglob "j" robota. Neka je u pitanju rotacioni zglob pokretan rotacionim hidrauličnim motorom. Izlazni momenat motora (P_mj) je jednak pogonskom momentu u zglobu (P_j) ukoliko je veza direktna. Tako je:

Ako je veza ostvarena preko para zupčanika odnosa  tada je:

Slično važi i za vezu obrtanja motora (ugao ) i obrtanja zgloba (ugao ). Ako je veza direktna tada je:

=

a ako postoji zupčasti par tada je:

Sl. 3.27. Pogon translatornog zgloba

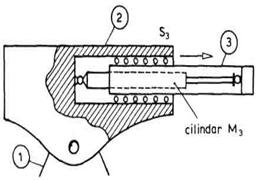
Veća raznolikost je u slučaju primene hidrauličnih cilindara dakle motora koji proizvode translatorno kretanje. Prikazaćemo to sa nekoliko primera.

U prvom primeru (sl. 3. 27) posmatraćemo translatorni zglob S₃ jednog zamišljenog robota. Sam zglob realizovan je u vidu jednog duguljastog segmenta (segment 3 na slici) koji se izvlači kroz odgovarajuće ležište postavljeno na segmentu 2. Hidraulični motor M₃ direktno pokreće zglob tako što je cilindar vezan za segment 2, a klip za segment 3.

Očigledno da je ovde izlazna sila klipa, u stvari, pogonska     sila zgloba (), a pomeranje u zglobu jednako je pomeranju klipa ().

Sl. 3.28. Dve mogućnosti pogoni rotacionog zgloba

Sledeći primer predstavlja jedno rešenje pogona rotacionog zgloba. Neka je to neki zglob  (sl. 3.28a). Cilindar se vezuje za segment "j-1" a klip za segment "j"na način prikazan na slici. Ovo je vrlo čest način postavljanja hidrauličnih cilindara. Karakteristično je da postoji nelinearna veza između kretanja klipa (pomeranje s_j) i obrtanja zgloba (ugao q_j )kao i između pogonske sile klipa (F_Mj) i odgovarajućeg momenta oko ose zgloba (P_j).

Druga mogućnost za pogon rotacionog zgloba prikazana je na slici 3.28.(b). U pitanju je pogon preko zupčaste letve. U ovom slučaju veza između kretanja klipa i obrtanja zgloba je linearna. Primer je dat za slučaj pokretanja prvog zgloba S1

3.6. PNEUMATSKI POGON

Razmotrimo na kraju pneumatski pogon robota. To je jedan od najstarijih načina pokretanja robota. Pneumatski pogon zasniva se na pokretanju klipa u cilindru pomoću pritiska komprimovanog vazduha. Dakle, način rada je unekoliko sličan hidrauličnom pogonu ali uz bitnu napomenu - vazduh je, za razliku od ulja, stišljiv. Još treba naglasiti da pneumatski pogon radi sa znatno nižim pritiscima nego hidraulični.

Sl. 3.29. Cilindri jednosmernog i dvosmernog dejstva

Danas se pneumatski pogon kod robota sreće prilično retko. Glavni problem je u regulisanju kretanja, odnosno u ostvarivanju željenog kretanja klipa (zadata promena brzine). Zato se pneumatski pogon prvenstveno nalazi kod prostih industrijskih manipulatora. U tim primenama klip u cilindru se pod pritiskom kreće od jednog kraja do drugog po nekom nelinearnom zakonu na koji ne utičemo. To je često dovoljno za prosto premeštanje radnih predmeta.Objasnićemo ukratko ovakav rad pneumatskog cilindra, mada treba reći da se u poslednje vreme razvijaju i uspešni pneumatski servosistemi.Komprimovani vazduh se, po pravilu, dobija iz glavnog fabričkog kompresora, odnosno rezervoara smeštenih u njegovoj blizini. 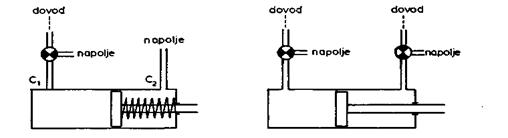Fabrička razvodna mreža obezbeđuje komprimovani vazduh na radnom mestu robota-manipulatora.Pneumatski cilindar može biti jednosmernog i dvosmernog dejstva. Cilindar jednosmernog dejstva može proizvoditi silu samo pri kretanju u jednom smeru (sl. 3.29a).  Kretanje u drugom smeru vrši se pod dejstvom povratne opruge.  Ulazni otvor označen je sa C₁, a C₂ je izlazni otvor kroz koji se vazduh ispušta u spoljašnju sredinu. Naime, kod pneumatskog pogona, za razliku od hidrauličnog, radni fluid se ne vraća u rezervoar pa nema povratnog voda. Kod cilindra dvosmernog dejstva (sl. 3.29b) vazduh pod pritiskom može da se dovodi i na otvor C₁ i na otvor C₂. Tako se može ostvariti sila u oba smera.

Sl. 3.30. Princip rada pneumatskog cilindra

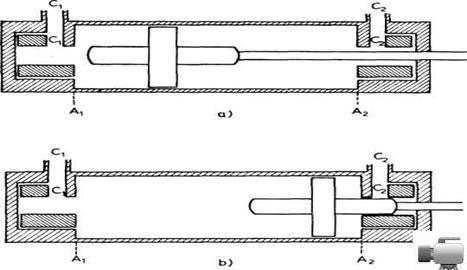
Šema cilindra sa klipom prikazana je na slici 3.30. Kada se vazduh pod pritiskom pusti kroz otvor C₁ klip se brzo pokreće u smeru od A₁ ka A₂ (udesno na slici 3.30a). Vazduh koji se nalazio u cilindru sa desne strane klipa ističe pri tome kroz otvor C₂. Kada klip dođe u neposrednu blizinu položaja A₂, istureni deo klipa zatvoriće široki prolaz otvora C₂ (sl. 3.30b). Ipak, vazduh nastavlja da ističe kroz uski prolaz otvora. Ovo isticanje kroz uski prolaz je znatno sporije, pa će doći do sabijanja vazduha sa desne strane klipa što će bitno usporiti kretanje klipa. Tako, klip će konačno stići u položaj A₂ ali neće udariti velikom brzinom. Ovakvo usporenje bilo je neophodno da bi se izbegao jak udar i oštećenje cilindra. Ako se na otvor C₂ stave dopunski prigušivači, može se postići sporije pomeranje klipa u cilindru celim putem kretanja.

Treba, na kraju, spomenuti i neke komponente koje se po pravilu sreću kod pneumatskog pogona: uređaji za filtriranje i lubrifikaciju vazduha, prigušivači buke itd. Prigušivače buke posebno spominjemo jer pneumatski pogon karakteriše jaka buka koja nastaje prilikom ispuštanja vazduha u spoljašnju sredinu.

3.7. KOMPENZACIJA STATIČKOG OPTEREĆENJA

Posmatrajmo laktasti robot prikazan na slici 3.31. Sada analizirajmo sile koje prave momenat oko pojedinih zglobova, odnosno proizvode opterećenje zglobova. Na sve delove robota deluje sila težine što je prikazano strelicama na slici 3.31 i te sile prave momenat oko zglobova S₂ i S₃ . Ovo opterećenje nazivamo statičkom komponentom opterećenja. Pored sila težine, momenat oko zglobova prave i sile inercije nastale prilikom kretanja robota. Momenti inercijalnih sila čine dinamičku komponentu opterećenja.

Sl. 3.31. Statičko opterećenje laktastog robota

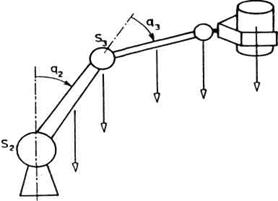
Kako je statička komponenta uvek prisutna to je logično razmišljati kako da se izvrši uravnoteženje, odnosno kako da se kompenzuju momenti nastali usled težina. Jedan načina je metoda kontra težina. Ta ideja je već spominjana i primenjena pri postavljanju motora za pogon šake (vidi sliku 3.5b). Motori za pogon šake postavljaju se sa suprotne strane zgloba lakta. Tako predstavljaju kontratežinu koja delimično uravnotežuje težinu segmenta 3, šake i radnog predmeta. Ovo je svakako korisno, ali s obzirom na težinu motora veći deo statičkog opterećenje oko zgloba lakta ostaje neuravnotežen. Da bi kompenzacija bila potpuna trebalo bi da kontratežina bude dovoljno velika. Međutim, to bi znatno povećalo ukupnu težinu robota, a time i dinamičko opterećenje pri radu. Za slučaj zgloba lakta često se zadovoljavamo ovakvom delimičnom kompenzacijom pa motor mora savladati nekompenzovani deo statičkog opterećenja i ćelo dinamičko opterećenje. To, međutim, nije dobro rešenje u slučaju robota za rad sa većim teretima. Tada se pristupa kompenzaciji pomoću posebnog mehanizma što će biti objašnjeno u sledećoj analizi.

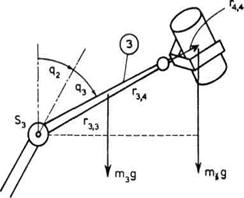
Posmatraćemo zglob lakta (S₃). Sile težina koje prave momenat oko ovog zgloba prikazane su, u nešto pojednostavljenom slučaju, na slici 3.32. Momenat statičkog opterećenja sada je:

k

                                                                (3.29)

gde je m₃ masa segmenta 3, a  masa kompletne šake sa radnim predmetom. Momenat je proporcionalan sinusu ugla q₂ + q₃, a to je ugao nagiba segmenta 3 u odnosu na vertikalu. Promena momenta u zavisnosti od ugla nagiba prikazana je na slici 3.33 punom linijom.

Sl. 3.32. Statičko opterećenje lakta

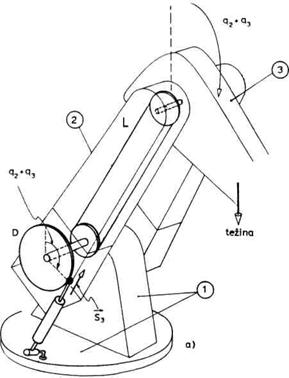
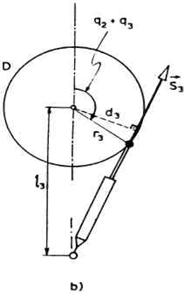
Mehanizam za kompenzaciju prikazan je na sl. 3.34. Ovo je u stvari modifikacija mehanizma prikazanog na slici 3.14a namenjenog za pogon zgloba 3 odnosno pokretanje segmenta 3. Obrtanje segmenta 3 prenosi se preko prenosnog lanca L i tako se obrće disk D. Primetićemo da se disk obrće za isti ugao za koji se segment 3 obrne u odnosu na vetikalu, a to je ugao q₂ + q₃. Za obod diska vezan je klip pneumatskog ili hidrauličnog cilindra koji se naziva kompenzator. Gas ili ulje u cilindru vrši pritisak na klip i proizvodi silu kompenzacije S₃. Ova sila pravi kontramomenat oko osovine diska. Kontramomenat se preko lanca prenosi do zgloba lakta i poništava momenat težine segmenta 3 i šake.

Sl. 3.33. Promena momenta opterećenja i momenta kompenzacije u zavisnosti od ugla nagiba

Razmotrimo sada jedan specijalni slučaj. Pretpostavimo da je obezbeđen konstantan pritisak u cilindru, bez obzira na pomeranje klipa. Ovo je približno tačno kod hidrauličnog cilindra vezanog za hidraulični akumulator jer je promena zapremine radnog gasa uočljivo manja od ukupne zapremine gasa. Spomenimo da u slučaju pneumatskog cilindra (punjenog određenom količinom gasa) ovo ne važi jer se pri sabijanju gasa povećava pritisak.

Zadržaćemo se na objašnjenju pomenutog specijalnog slučaja. Rekli smo da je u cilindru stalan pritisak i da će sila S₃ kojom deluje klip biti takođe stalna bez obzira na položaj robota. Momenat kompenzacije M_k3 biće:

          (3.30)

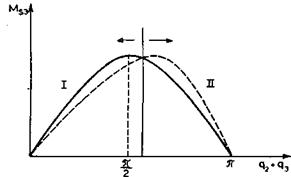
Sa slike (3.34b) vidimo da se pri obrtanju segmenta 3, a time i diska D menja krak sile kompenzacije označen na slici sa d. Može se pokazati da se krak d₃ menja po zakonu:

  (3.31)

a momenat kompenzacije onda po zakonu:

                      (3.32)

Sl. 3.34. Kompenzacija zgloba lakta

Ova promena momenta kompenzacije u zavisnosti od ugla q₂ + q₃ prikazana je na slici 3.33 isprekidanom linijom. Sa slike 3.33 vidimo da momenat statičkog opterećenja (puna linija) i kontramomenat usled kompenzacije ne mogu potpuno da se ponište. Podešavanjem pritiska u kompenzacionom cilindru, a time menjajući silu S₃, postižemo što bolje poklapanje ova dva grafika. Pošto su momenti suprotnih smerova, vidimo da će se u velikoj meri poništiti. Tako će motoru preostati da savlada samo manji deo statičkog opterećenja (tamo gde je ono veće od kompenzacije, a to je deo I) ili pak da savlada višak kompenzacije (tamo gde je ona prevelika i veća od statičkog opterećenja - deo II).

Sl. 3.35. Statičko opterećenje ramena.

Prelazimo na analizu problema kompenzacije statičkog opterećenja ramenog zgloba S₂. Posmatraćemo zglob S₂ i sile težina koje proizvode statičko opterećenje oko ose zgloba (sl. 3.35). Masa segmenta 2 je m₂. Ako zamislimo razdvajanje segmenata 2 i 3 u zglobu S₃, tada dejstvo segmenta 3 na segment 2 posmatramo preko sile F_s3 koja je jednaka:

                           (3.33)

i momenta statičkog opterećenja lakta koji je dat izrazom (3.29). Ovo je prikazano na slici 3.35(b). Sada je statičko opterećenje ramena S₂:

Ovde treba uočiti dva slučaja. Prvi nastupa onda kada nije uvedena kompenzacija lakta

k

                     (3.34)

S₃, a drugi ako je ova kompenzacija uvedena. U prvom slučaju izraz (3.34) važi u celosti i takav momenat ramena teško se može poništiti kontramomentom kompenzacije u ramenu. U drugom slučaju kompenzacija poništava najveći deo momenta M_s3 pa se samo njegov mali deo prenosi na segment 2. Ako bi pojednostavili smatrajmo da je poništavanje u laktu potpuno i tada se u izrazu (3.34) neće pojaviti M_s3 a izraz će postati:

                        (3.35)

iz čega sledi da je momenat statičkog opterećenja ramena proporcionalan sinusu ugla q₂. U daljoj analizi zadržaćemo se na ovom slučaju. Ostaje činjenica da je statičko opterećenje lakta potpuno kompenzovano.

Sl. 3.36. Kompenzacija  ramenog zgloba

Matematički gledano, postupak je isti kao i u slučaju kompenzacije lakta. Ako bismo posmatrali konstruktivno, rešenje je ovde mnogo jednostavnije jer nije potreban nikakav prenosni mehanizam. Kompenzacioni cilindar vezuje se za segmente 1 i 2 na način kako je prikazano na slici 3.36.

Opterećenja data izrazima (3.29) i (3.35) i kompenzacije prikazane na slikama 3.34(b) i 3.36(b) dovode do zaključka da je problem kompenzovanja opterećenja ramena matematički sličan problemu koji smo obrađivali pri kompenzovanju lakta, samo što se u slučaju ramena pojavljuje ugao q₂, a u slučaju lakta ugao q₂ + q₃. Sledi da za momenat kompenzacije u ramenu dobijamo izraz:

               (3.36)

gde je S₂ sila klipa koji vrši kompenzaciju (sl. 3.36).

Ako bismo opterećenje M_s2 i kontramomenat M_k2 prikazali grafički dobili bismo dijagrame kao na slici 3.33, s tim što bi u ovom slučaju momenti zavisili samo od ugla q₂. Podešavanjem pritiska u kompenzacionom cilindru menjamo silu S₂, te tako postižemo približno poklapanje ovih dijagrama. U tom slučaju najveći deo statičkog opterećenja ramena poništen je kompenzacijom.